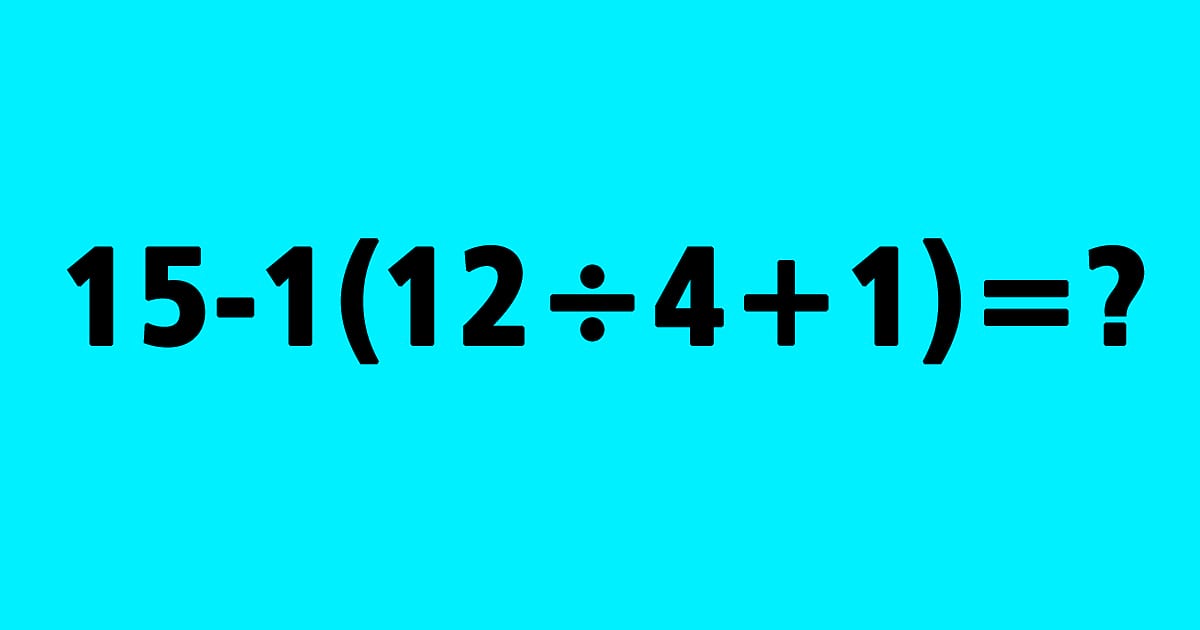Rovnice jsou jedním ze strašáků školou povinných dětí, zejména pokud jsou koncipovány do složitějších útvarů používajících vícero matematických operátorů, či dokonce proměnné. Každá matematická operace má svá specifická pravidla a operátory se používají vždy stejným způsobem a na základě stejných zákonů. Přestože se může stát, že by rovnice měla více řešení (zvláště pohybujeme-li se v celém spektru číselné osy), jsou tato řešení vždy jednoznačná, jelikož jsou dána přijatými matematickými postupy.
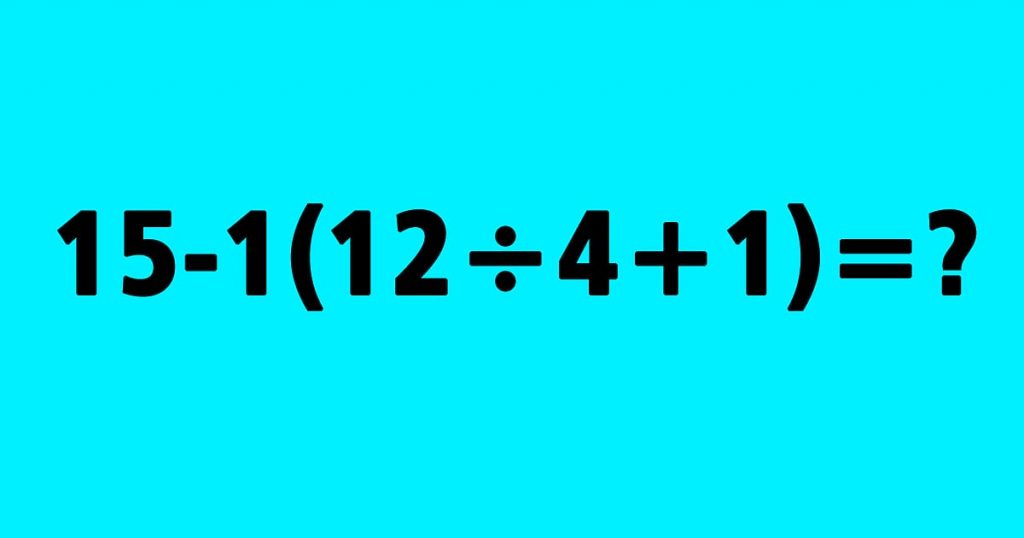
Dokážete následující rovnici vyřešit správně?
Zkuste spočítat následující rovnici:
15 – 1(12 / 4 + 1) =
Rovnice se může jevit jako jednoduchá, pro její správné řešení je však potřeba využít správného přístupu. Pokud vám vyšel výsledek 11, pravděpodobně jste počítali správně, řada lidí však při výpočtu zapomene používat jednoduché pravidlo upřednostňování a komutativnosti jednotlivých operací. Pojďme se tedy podívat, jakým způsobem by mělo být k výpočtu přistupováno.
PEMDAS neboli ZENDSO
PEMDAS je pravidlo, jež definuje vzájemné upřednostňování matematických operací v rámci jednoho zápisu a chronologii jejich řešení. Tato zkratka pochází z angličtiny a do češtiny by se dala přeložit jako ZENDSO, tedy:
- Závorky
- Exponenty
- Násobení
- Dělení
- Sčítání
- Odčítaní
Seřazení uvedených operací udává jejich aplikaci v rámci výpočtu, tzn. pokud bychom chtěli řešit náš příklad, je potřeba postupovat podle kroků uvedených níže.
Jak správně rovnici vypočítat
V naší rovnici máme v závorce uvedeno:
(12 / 4 +1)
Abychom vyřešili závorku, je nutné aplikovat chronologii dalších operací – tedy upřednostníme dělení před sčítáním a vyjde nám 3 + 1 = 4, což je výsledek závorky. Nyní má tedy rovnice tvar:
15 – 1 x 4 =
Pokud mezi číslem a závorkou není znaménko, automaticky se předpokládá, že se jedná o operaci násobení. Podle pravidla PEMDAS je nyní potřeba rozhodnout, která operace má přednost, jelikož by jejich záměna zcela změnila výsledek. Jak lze odvodit, násobená má přednost před odčítáním, nejdříve tedy vyřešíme úkon1 x 4 = 4. Tento výsledek pak doplníme do odečtu, tedy 15 – 4 = 11.

Jak je z výpočtu patrné, při dodržování uvedeného pravidla se prakticky nedá splést a funguje vždy, jelikož je založeno na zavedených pravidlech matematiky.